問題
実在気体に関する次の記述の下線部のうち, 最も不適切なものはどれか。
実在気体の PV 線図（横軸：体積V、縦軸：圧カ P）において、高温での等温線は理想気体における ① ボイルの法則 からほんの少しずれるに過ぎない。 ある温度以下で温度一定のまま圧縮すると、ある圧力で気体は凝縮して液体を生じ始め、体積が減少していく。すべての気体が液体になるまで圧力は一定のままであり、このときの圧力はこの温度における ② 平衡蒸気圧 である。つまり、液体を生じ始め、気体すべてが液体になるまでの領域は、気液2相が平衡を保っている領域であり、この間圧力が一定であることは、ギブスが導出したの ③ 相律 から ④ 自由度(可変度) 0 として説明できる。
気液2相領域の頂点と接する等温線の温度を臨界混度といい、液化させるためには温度を ⑤ 臨界温度以下 にする必要がある。
解答
実在気体の性質に関する問題。
以下に各項目の正否を記す。
①正しい
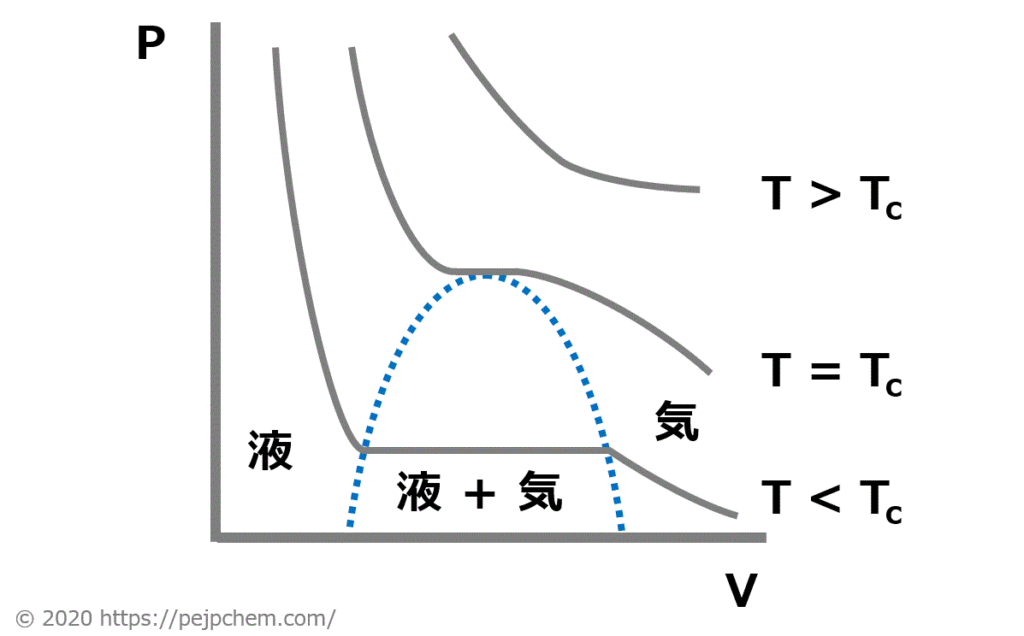
実在気体のPV線図を以下に示す。下図より、T > Tc の領域では P は V に反比例する様な外形のグラフとなっている。この事から 、T > Tc の領域ではボイルの法則（PV=一定）からほんの少しずれるに過ぎない。よって①は正しい。
②正しい
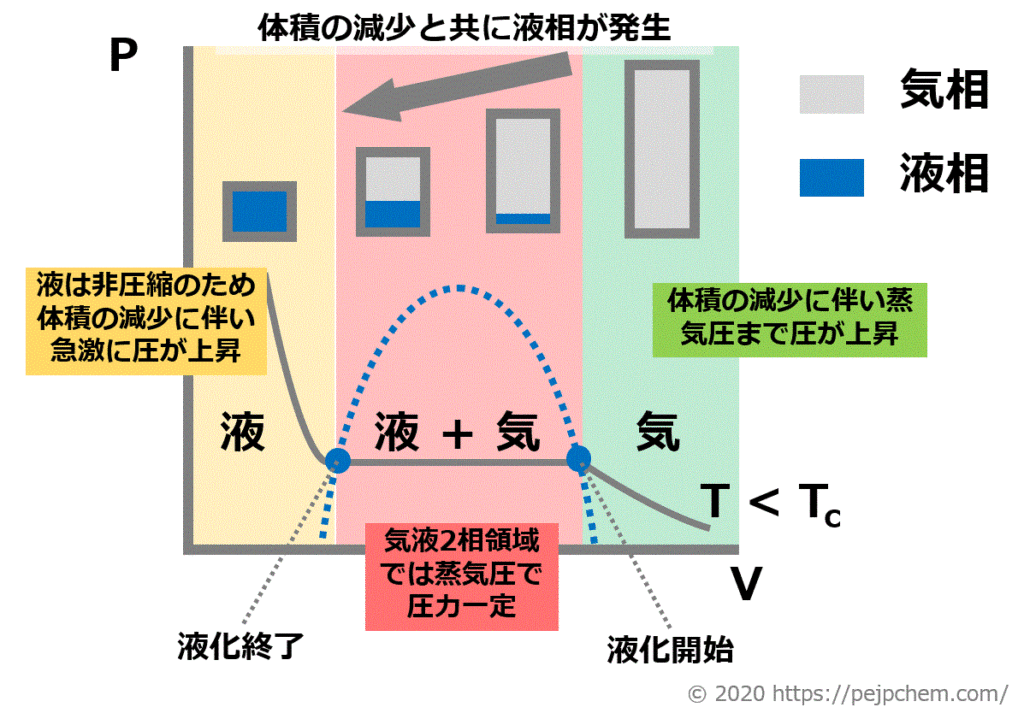
以下に T < Tc (Tは一定)において、体積を減少させた際の実在気体の系に起こる現象を模式的に記した図を示す。右端から体積を小さくしていくと青色点線のに触れるまで圧が上昇し、青色点線の右側と接したとこから液化が始まる。その後、体積の減少に伴い液化が進み、青色点線左側の範囲で全て液となる。この、圧力一定の範囲における圧力は温度固有の蒸気圧となる。以上より②は正しい。
③正しい
設問の内容として③が正しくないとすると、前後の “ギブスが導出した”と“自由度(可変度) 0 ”との文章が成り立たなくなる。よって、③は正しい。
④誤り
ギブスの相律は 自由度：F、成分数：n、フェーズの数：Ph より F = n + 2 – Ph で計算できる。 今回計算する範囲はフェーズの数：Ph ＝ 2であり、成分数：n =1 の場合を考えると、 F = 1 + 2 – 2 = 1 となる。よって、④は誤り。
⑤正しい
理想気体は臨界温度以下にしないと液化出来ない。よって⑤は正しい。
以上より ④ 自由度(可変度) 0 が間違いである。
答え ④ 自由度(可変度) 0